本节书摘来异步社区《OpenGL ES 2.0游戏开发（上卷）：基础技术和典型案例》一书中的第6章，第6.3节，作者： 吴亚峰 责编： 张涛，更多章节内容可以访问云栖社区“异步社区”公众号查看。

6.4 点法向量和面法向量OpenGL ES 2.0游戏开发（上卷）：基础技术和典型案例本章前面几节的案例都是基于球面开发的，球面属于连续、平滑的曲面，因此面上的每个顶点都有确定的法向量。但现实世界中的物体表面并不都是连续、平滑的，此时对于面上的某些点的法向量计算就不那么直观了，图6-18说明了这个问题。

从图6-18中可以看出，顶点A位于长方体左、上、前3个面的交界处，此处是不光滑的。这种情况下顶点A的法向量有两种处理策略，具体如下所列。

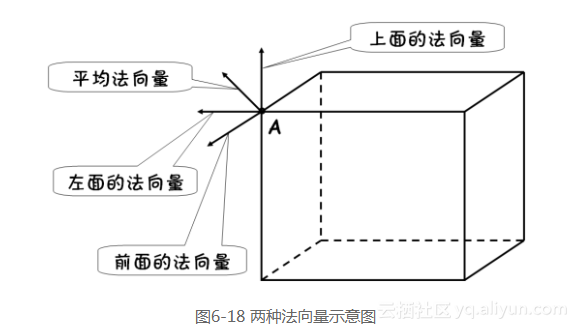
在顶点A的位置放置3个不同的顶点，每个顶点看作是仅属于一个面。各个顶点的法向量即为其属于的面的法向量，这种策略就是面法向量的策略，比较适合棱角分明的物体。

顶点A的位置仅认为存在一个顶点，其法向量取其所属的所有面法向量的平均值。这种策略就是点法向量策略，比较适合用多个平面搭建平滑曲面的情况。

提示

前面球体的案例采用的就是此策略，只不过由于球面上顶点的法向量可以直接计算，因此相当于直接得到了点平均法向量，而略去了计算平均值的过程。但很多情况下是需要进行平均法向量的计算的，尤其是在加载预制3D模型的时候，这一点在后面的章节会有专门的介绍。

了解了点法向量和面法向量的基本知识后，下面将通过两个基本相同的绘制立方体的案例（Sample6_7和Sample6_8）对这两种策略进行比较。这两个案例的运行效果如图6-19和图6-20所示，其中图6-19来自采用面法向量策略的案例Sample6_7，图6-20来自采用点法向量策略的案例Sample6_8。

说明

从图6-19与图6-20的比较中可以看出，对于棱角分明的物体适合采用面法向量策略。若采用点法向量策略渲染真实感就会差很多了，实际开发中读者应该根据所绘制物体表面的特点来选用合适的策略。

了解了两个案例的运行效果后，就可以进行案例的开发了。由于这两个案例中大部分的代码与前面6.2.5小节中案例Sample6_5里的完全相同，主要的区别就在立方体顶点与法向量初始化的部分，所以下面仅给出Sample6_7与Sample6_8中初始化立方体顶点与法向量的部分代码，具体内容如下所列。

（1）首先介绍采用面法向量策略的案例Sample6_7中初始化立方体顶点及法向量数据的initVertexData方法，其代码如下。

1　　public void initVertexData() {　　　 //初始化顶点数据的方法2　　　　　   vCount=6*6;　　　　　　　　　 //顶点数(6个面，每个面两个三角形，6个顶点)3　　　　　   float vertices[]=new float[]{4　　　　　　　Constant.UNIT_SIZE,Constant.UNIT_SIZE,Constant.UNIT_SIZE,　　　//立方体前面5　　　　　　　-Constant.UNIT_SIZE,Constant.UNIT_SIZE,Constant.UNIT_SIZE,　　//两个三角形6　　　　　　　-Constant.UNIT_SIZE,-Constant.UNIT_SIZE,Constant.UNIT_SIZE,　　//中6个顶点7　　　　　　　Constant.UNIT_SIZE,Constant.UNIT_SIZE,Constant.UNIT_SIZE,//的_x_、_y_、_z_坐标8　　　　　　　-Constant.UNIT_SIZE,-Constant.UNIT_SIZE,Constant.UNIT_SIZE,9　　　　　　　Constant.UNIT_SIZE,-Constant.UNIT_SIZE,Constant.UNIT_SIZE,10　　　　 　　 　　……//此处省略了其他5个面顶点坐标产生的代码，11　　　　　　     ……//需要的读者请自行查看随书光盘中的源代码12　　　　　};13　　　　ByteBuffer vbb = ByteBuffer.allocateDirect(vertices.length * 4);　　　　　　　　　　　　　　　　　　　　　　　　　　　　//创建顶点坐标数据缓冲14　　　　vbb.order(ByteOrder.nativeOrder());　 //设置字节顺序15　　　　mVertexBuffer = vbb.asFloatBuffer();　//转换为float型缓冲16　　　　mVertexBuffer.put(vertices);　　　　　 //向缓冲区中放入顶点坐标数据17　　　　mVertexBuffer.position(0);　　　　　　　//设置缓冲区起始位置18　　　　float normals[]=new float[]{19　　　　　　0,0,1,　0,0,1,　0,0,1,　0,0,1,　0,0,1,　0,0,1,　　//前面上6个顶点的法向量20　　　　　　0,0,-1,　0,0,-1,　0,0,-1,　0,0,-1,　0,0,-1,　0,0,-1,//后面上6个顶点的法向量21　　　　　　-1,0,0,　-1,0,0,　-1,0,0,　-1,0,0,　-1,0,0,　-1,0,0,//左面上6个顶点的法向量22　　　　　　1,0,0,　1,0,0,　1,0,0,　1,0,0,　1,0,0,　1,0,0, 　　//右面上6个顶点的法向量23　　　　　　0,1,0,　0,1,0,　0,1,0,　0,1,0,　0,1,0,　0,1,0, 　　//上面上6个顶点的法向量24　　　　　　0,-1,0,　0,-1,0,　0,-1,0,　0,-1,0,　0,-1,0,　0,-1,0,//下面上6个顶点的法向量25　　　　};26　　　　 ByteBuffer nbb = ByteBuffer.allocateDirect(normals.length*4);　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　//创建绘制顶点法向量缓冲27　　　　 nbb.order(ByteOrder.nativeOrder());　　　　　//设置字节顺序28　　　　 mNormalBuffer = nbb.asFloatBuffer();　　　　 //转换为float型缓冲29　　　　 mNormalBuffer.put(normals);　　　　　　　　　　//向缓冲区中放入顶点法向量数据30　　　　 mNormalBuffer.position(0);　　　　　　　　 　　//设置缓冲区起始位置31　　}

• 第3-17行为立方体各顶点位置数据的初始化。
• 第17-30行为立方体各顶点法向量数据的初始化，其中给每个顶点设置了其所属面的法向量。

（2）接着介绍采用点法向量策略的案例Sample6_8中初始化立方体顶点及法向量数据的initVertexData方法，其代码如下。

1　　public void initVertexData() {　　　　　　　　//初始化顶点数据的方法2　　　　vCount = 6 * 6; 　　　　　　　　　　　　　　//顶点数3　　　　float vertices[] = new float[] {4　　　　　　……//此处省略了初始化立方体6个面各个顶点坐标数据的代码，5　　　　　　……//需要的读者请自行查看随书光盘中的源代码6　　　　};7　　　　ByteBuffer vbb = ByteBuffer.allocateDirect(vertices.length * 4);　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　     //创建顶点坐标数据缓冲8　　　　vbb.order(ByteOrder.nativeOrder());　　　　　　　//设置字节顺序9　　　　mVertexBuffer = vbb.asFloatBuffer();　　　　　　//转换为float型缓冲10　　　　mVertexBuffer.put(vertices);　　　　　　　　　　//向缓冲区中放入顶点坐标数据11　　　　mVertexBuffer.position(0);　　　　　　　　　　　//设置缓冲区起始位置12　　　　float normals[] = vertices;　　　　　　　　　　//顶点法向量数据13　　　　ByteBuffer nbb = ByteBuffer.allocateDirect(normals.length * 4);　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　   //创建绘制顶点法向量缓冲14　　　　nbb.order(ByteOrder.nativeOrder());　　　　　//设置字节顺序15　　　　mNormalBuffer = nbb.asFloatBuffer();　　　　 //转换为float型缓冲16　　　　mNormalBuffer.put(normals);　　　　　　　　　　//向缓冲区中放入顶点法向量数据17　　　　mNormalBuffer.position(0);　　　　　　　　　　 //设置缓冲区起始位置18　　}

提示

由于本案例中原始情况下将立方体的几何中心放在了坐标原点，因此，每个顶点的平均法向量就没有必要真正进行求和再平均的计算了，直接采用顶点的x、y、z坐标代替即可。但开发中并不总是像本章的案例一样可以进行简化，后面的章节会给出需要详细计算的案例。